Maratón
Yo mismo, en alguna ocasión he querido rendir culto a Filípides y recordar su gesta.
Maratón from DIEGOMECAALVAREZ
Aquiles, el primero de los héroes
Una vez que has leído la lectura, responde a las siguientes preguntas.
COPIA CON BUENA LETRA Y SIN FALTA DE ORTOGRAFÍA LOS ENUNCIADOS Y RESPONDE:
1.- ¿ De quién era hijo Aquiles ?
2.- Menelao pidió a Odiseo que reclutara a los principales héroes. ¿ A quién reclutó el primero?
3.- ¿ Quién era el rey de Esparta?
4.- Aquiles se enamoró de Deidamía¿ Cómo se llamaba el hijo que tuvo Aquiles con Dedamía?
5.- "Morirás , hijo, frente a las murallas de Troya" ¿ Quién le dijo estas palabras a Aquiles?
6.- En el décimo año de la guerra de Troya, Aquiles dejó de luchar. ¿ Por qué ?
7.- Mientras que Aquiles permanecía en su tienda, Patroclo lucho de manera formidable hasta que fue herido mortalmente y murió. ¿ Quién lo hirió ?
8.-¿ Qué hizo Aquiles tras la muerte de Patroclo ?
9.- Según la mitología, el dios Apolo , que no amaba al hijo de Tetis ( Aquiles) , guió el dardo que lanzaron a su talón, el único punto que no fue bañado por las aguas del Estige, pues era el sitio por donde la diosa Tetis habia sujetado a su amado hijoo para evitar que el río se lo llevara. ¿ Qué pasó en realidad? ¿ Quién lanzó la fecha que lo hirió mortalmente?
10.- Resume brevemente las ideas principales del texto.
No te confundas: Potencias
Copia estas sencillas reglas en tu cuaderno. 
¡ Apréndetelas !
Realiza los siguientes ejercicios, sólo tienes que aplicar las reglas que has copiado.
Realiza los siguientes ejercicios, sólo tienes que aplicar las reglas que has copiado.
Operaciones combinadas
Dibuja la pirámide en tu cuaderno.
Debes respetar el orden que se te indica a la hora de hacer las operaciones.
Ahora copia los siguientes ejercicios en tu cuaderno y aplica la pirámide anterior.
Copia y realiza las siguientes operaciones
Copia Y Realiza las siguientes actividades en tu cuaderno.
COPIA ESTE CUADRO EN TU CUADERNO.
REALIZA LAS SIGUIENTES OPERACIONES:
a.- 234,5 + 3,5 + 0,98 + 89,345 =
b.- 8483,4 + 939,4 + 0,3939 + 0,9 =
c.- 48,493 - 939,94 + 98 + 9,9 =
d.- 8483,4 + 9 + 393 + 9,5 =
e.- 84848, 949 - 0,98 =
f.- 93,48 - 23,893 =
g.- 939,4 - 4,345 =
h.- 9493,4 - 0,933 =
i.- 938,5 - 9,383 =
¿ Cómo se multiplican los decimales ?
COPIA ESTE EJEMPLO EN TU CUADERNO.
REALIZA LAS SIGUIENTES ACTIVIDADES EN TU CUADERNO.
DEMUESTRA QUE LO HAS APRENDIDO Y RESUELVE LAS SIGUIENTES OPERACIONES:( Ronaldo todas X 2).
A.- 23,4 X 3,2 =
B.- 898,4 X 3,2 =
C.- 982,3 X 3 =
C.- 234,6 X 4,3 =
D.- 44,32 X 4,3 =
E.- 342,4 X 4,4 =
RESUELVE ESTAS SENCILLAS DIVISIONES:
( Ronaldo todas X 2 ).
A.- 2345 : 2 =
B.- 342,3 : 3 =
C.- 23,44 : 2 =
D.- 422,1 : 4 =
E.- 42,24 : 4 =
F..- 4,325 : 4 =
Kathrine Switzer: Primera mujer en correr un maratón.
Ninguna mujer había corrido (estaba prohibido) oficialmente la maratón de Boston.
En
el otoño norteamericano de 1966, Kathrine Switzer le comenta a su coach
Arnie Briggs (un maratonista de 50 años), sus ganas de participar en la
nueva edición de la Boston Marathon. Kathrine entrenaba en el equipo
masculino de Cross Country de la Universidad de Siracusa, dado que no existían equipos femeninos intercolegiales en esos tiempos.
Arnie le dice que no cree que una mujer haya sido capaz de correr 26.2
millas, más allá de la publicidad que rondaba, pero que si ella
entrenaba como para hacerlo, la acompañaría. Kathy entrenó duro, y en
Marzo de 1967 solicitaron los formularios. En ningún lugar se
especificaba el sexo, y Kathy llenó con sus iniciales los espacios en
blanco en donde irían sus nombres: K.V. Switzer. Pagaron los 3 dólares
(era el costo por inscripción en ese entonces), y enviaron los papeles
de inscripción. Durante las primeras millas nada ocurrió. Junto a ellos también
corría Tom, el novio de Kathy.
Luego de recorridas las dos primeras
millas, un camión de medios delató la presencia de Katherine. Jock
Semple, el Co-director del Maratón, se volvió furioso cuando vio a
Kathy, y se abalanzó sobre ella gritándole -“Get out of my race…!!!”-
(-“Fuera de mi carrera…!!!”-) Tom, el novio de Kathy, con un físico más
de rugbier que de maratonista, lo empujó derribando a Semple hacia un
costado. Los fotógrafos documentaron ese momento, que recorrió el mundo
entero. Kathy terminó su primer y accidentada maratón en 04:20, pero
había marcado un precedente.
Potencias
Potencias con exponente 0
Son aquellas que tiene como base un número y como exponente el cero o elemento neutro y equivalen a la unidad.
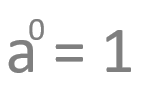
Vamos a ver un ejemplo: 2 elevado a 0 es igual a 1.
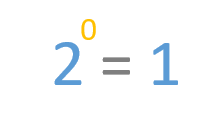
Potencias con exponente 1
Son aquellas que tiene como base un número y como exponente la unidad y son equivalentes a la base sin exponente. Sé que es algo muy evidente pero sigue siendo una peculiaridad de las potencias.
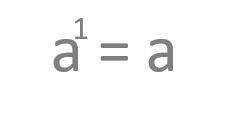
Vamos a ver un ejemplo: 2 elevado a 1 es igual a 2.
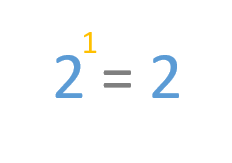
Producto de potencias con la misma base
En este caso, vamos a ver lo que ocurre cuando multiplicamos dos potencias que tienen la misma base (a) y, por contra, tienen exponentes diferentes (n y m). Esta expresión se puede simplificar con una potencia con la misma base y sumando ambos exponentes (n + m).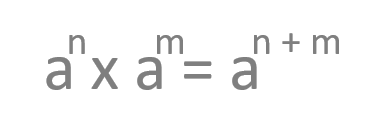 
Vamos a ver un ejemplo: Multipliquemos 2 elevado a 2 por 2 elevado a 3 y veremos como es lo mismo que 2 elevado a 5.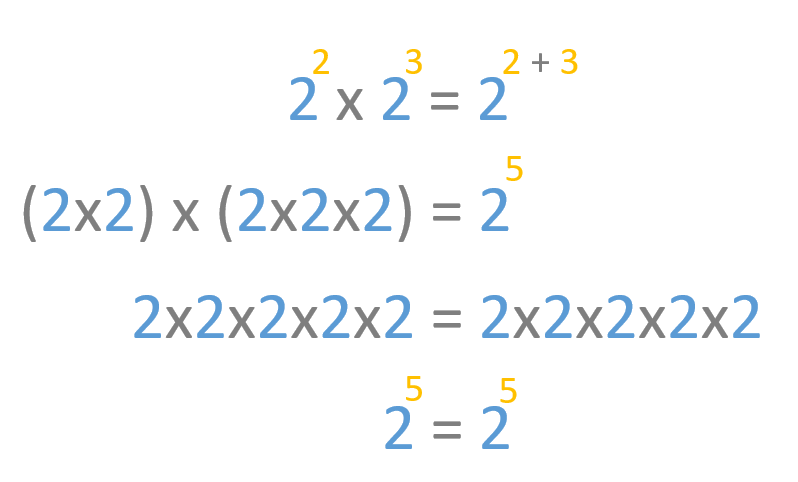
Producto de división con la misma base
En este caso, vamos a ver lo que ocurre cuando dividimos dos potencias que tienen la misma base (a) y, por contra, tienen exponentes diferentes (n y m). Esta expresión se puede simplificar con una potencia con la misma base y restando el exponente del dividendo al del divisor (n – m).
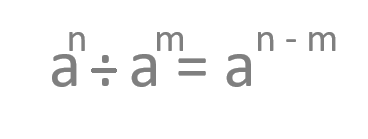
Vamos a ver un ejemplo: Dividamos 2 elevado a 4 entre 2 elevado a 2 y veremos como es lo mismo que 2 elevado a 2.
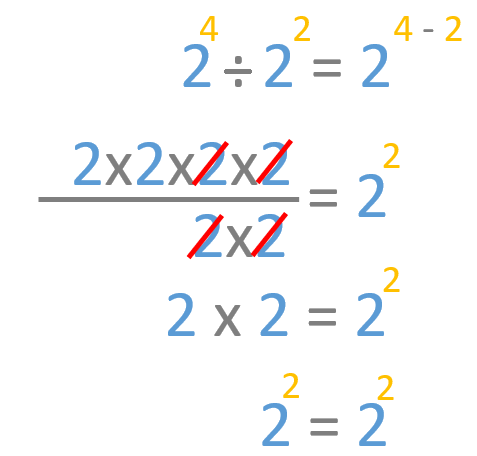
Potencias de exponente entero negativo
Es una propiedad únicamente valida cuando se trata de una potencia con base distinto a cero (0). Cuando nos encontramos con una base que cumpla esa condición y que tenga como exponente un número entero negativo, podemos decir que dicha potencia equivale a una fracción que tiene como numerador la unidad y que tiene por denominador la misma potencia pero cambiando el signo del exponente. (De negativo a positivo) 
Vamos a ver esta propiedad aplicada a un caso concreto. Veremos como 3 elevado a menos 2 es lo mismo que la fracción 1 como numerador y 3 elevado a 2 como denominador.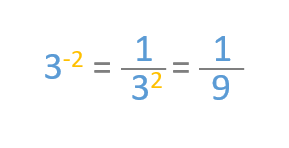
Potencias de otra potencia
En este caso veremos que una potencia de otra potencia, es lo mismo que una potencia con la misma base pero que como exponente tiene la multiplicación de ambos exponentes.
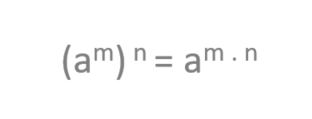
Continuamos con un ejemplo práctico en el que veremos que si elevamos 3 al cuadrado a 3, obtenemos el mismo resultado que si elevamos 3 a 6, en ambos casos, obtenemos el mismo resultado (729)
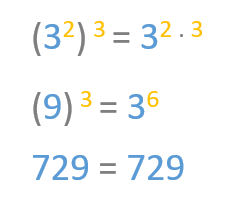
Multiplicación de potencias con el mismo exponente
En este caso vamos a comprobar que si nos encontramos una multiplicación de dos potencias con el mismo exponente, vamos a obtener el mismo producto que si multiplicamos primero las bases y luego el producto lo elevamos al exponente que comparten.
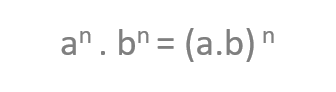
Ahora vemos un ejemplo en el que comprobamos que es lo mismo multiplicar 5 elevado a 3 por 3 elevado a 2, que multiplicar 5 por 3 y luego elevarlo a 2.
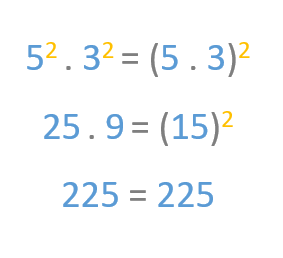
División de potencias con el mismo exponente
En este caso vamos a comprobar que si nos encontramos una división entre dos potencias con el mismo exponente, vamos a obtener el mismo cociente que si dividimos primero las bases y luego elevamos el cociente al exponente que comparten.
Ahora vemos un ejemplo en el que comprobamos que es lo mismo dividir 6 elevado a 2 entre 2 elevado a 2, que dividir 6 por 2 y luego elevarlo a 2.
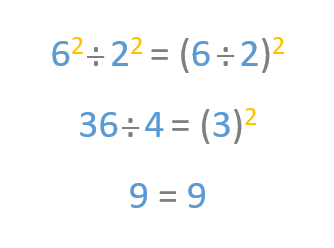
Fuente: https://www.smartick.es/blog/matematicas/recursos-didacticos/las-potencias/
Democracia
EL término "democracia" deriva de La unión de dos paLabras griegas: demos ("pueblo") y kratos ("gobierno"). Etimológicamente, entonces, democracia significa "gobierno del pueblo", es decir, gobierno ejercido y controlado por el conjunto del pueblo.
La democracia tuvo su origen en la Grecia antigua, especialmente en la polis de Atenas, entre los siglos VII y IV a.C. El órgano máximo del gobierno de la polis era la Asamblea, integrada por todos los ciudadanos libres. La cantidad reducida de habitantes y el hecho de que las mujeres y Los esclavos no participaran permitían que los ciudadanos pudieran reunirse en la plaza pública para discutir los asuntos públicos.
Actualmente, la democracia implica una serie de condiciones mínimas que permiten un acceso democrático a la toma de decisiones. Algunas de esas condiciones son:
- primacía de la decisión de la mayoría y el respeto de los derechos de las minorías;
- reconocimiento del derecho de toda persona a pensar diferente y expresarse de acuerdo con sus convicciones;
- realización de elecciones periódicas competitivas, libres, transparentes, con un voto personal, igual, secreto e informado, para que el pueblo decida quiénes deben ser sus gobernantes;
- garantía de competencia pacífica, a través del diálogo y la negociación entre las ideas y los grupos que se disputan el acceso al gobierno;
- distribución del poder que permita que las autoridades se controlen mutuamente y garantía de canales de expresión y fiscalización por parte del pueblo.
COPIA Y RESPONDE:
1.- ¿ De qué dos palabras proviene la palabra democracia?
2.- ¿ Qué significa la palabra "democracia"?
3.- ¿ Dónde se originó la democracia como sistema de gobierno?
4.- Explica con tus palabras las condiciones mínimas para que exista la democracia.
5.- ¿ Vivimos nosotros en la actualidad en democracia? ¿ Por qué?
Ponte las pilas: tablas 2,3 y 4.
a.-Escribe la tabla del 2 y 4.
b.- Resuelve las siguientes operaciones:
1.- 2243 X 4 =
2.- 9863 X 2 =
3.- 2365 X 42 =
4.- 3546 X 42 =
d.- Escribe la tabla del 3.
e.- Resuelve las siguientes operaciones:
1.- 2839 X 3 =
2.- 9839 X 3 =
3.- 8499 X 23 =
4.- 9398 X 23 =
f.- Resuelve las siguientes divisiones:
1.- 8287 : 4 =
2.- 8384 : 2 =
3.- 9929 : 4 =
4.- 9393 : 2 =
5.- 8287 : 3 =
6.- 8384 : 3 =
7.- 9929 : 3 =
8.- 9393 : 3 =
Remate final: Tablas de multiplicar
Antes de empezar, dale un buen repaso a las tablas de multiplicar. Puedes practicar con un compañero para que este te las pregunte.
1.- De abajo a arriba, escribe las tablas del 6,7,8 y 9. ( Inténtalo sin mirar en tu cuaderno ).
2.- Completa:
a.- 7 X .... = 28
b.- 7 X ... = 49
c.- 7 X ..... = 63
e.- 6 X .... = 24
f.- 9 X .... = 36
g.- 8 X .... = 48
h.- ... X .... = 81
i.- ... X .... = 54
3.- Practica las tablas con estas multiplicaciones:
a.- 0,789 X 7,8 =
b.- 0,9874 X 97 =
c.- 0,9887 X 96 =
d.- 0,8479 X 79 =
4.- Realiza las siguientes divisiones:
a.- 3897,7 : 9 =
b.- 69,384 : 8 =
c.- 59,874 : 9 =
d.- 98,789: 8 =
Troya
Una vez que has leído la lectura anterior, copia las siguientes preguntas en tu cuaderno y responde:
1.- ¿ Cuándo comenzó esta historia?
2.- ¿ En qué país actual está Troya?
3.- ¿Qué personaje de los que aparecen en la lectura fue amamantado por una osa?
4.- ¿ Entre que dos ciudades tubo lugar "la guerra de Troya"?
5.- ¿ Con quién se iba a casar Helena? ¿ Con quién se marchó?
6.- ¿ De quién era hermano Paris?
7.- ¿ Quién es Aquiles? ¿ Cuál era su punto débil ?
8.- ¿ Qué otros personajes de la historia te llaman la atención ? ¿ Por qué?
9.- ¿ Cómo murió Aquiles? ¿ Quién lo hirió mortalmente?
10.- ¿ Cómo consiguieron entrar los griegos en la ciudad de Troya?
Lee detenidamente el texto.
Después copia las preguntas que tienes a continuación y copia la opción correcta. ( No sólo la letra ).
Aquí puedes ver la película completa: ( No hace verdadero rigor histórico, pero podemos hacernos una idea de cómo ocurrieron los acontecimientos).
Repaso de Mates: 24 y Cía.
¡ No olvides copiar todos los enunciados! Es importante el orden y la presentación en el cuaderno.
Resuelve:
A.- 6398 X 7 =
B.- 5928 : 6 =
C.- 9879 : 7 =
D.- 8942 : 7 =
Una vez que has resuelto estas operaciones, llega el momento de empezar con la tabla del 8.
a.- Completa:
4x8=
2x8=
8x7=
8x5=
Hasta aquí ya deberías sabértelas. ¿ Qué nos tenemos que aprender? Resuelve y estudia:
8x8=
8x9=
9x9=
Piensa un poco:
¿ Qué número de la tabla del 8 da 64?¿Y 72 ?
Completa:
8x... = ...4
8x ...= 16
8x... = 24
8x ...= ..2
Coloca correctamente y resuelve:
a.- 987x8 =
b.- 784x8 =
c.- 667x8 =
d.- 896x8 =
e.- 788x8 =
f.- 65772:8 =
g.- 73569:8 =
h.- 74648:8 =
i.- 7998:8 =
Dale un poco a poco:
Nino Vargas y sus 7 amigos van al supermercado y compra 200 latas de refrescos con un importe total de 64,72€. ¿ Cuánto dinero tendrá que poner cada uno si pagan a partes iguales?
Repaso de Mates: Ronaldo y Nino Vargas
¡ No olvides copiar todos los enunciados! Es importante el orden y la presentación en el cuaderno.
Resuelve:
A.- 398 X 3 =
B.- 928 : 3 =
C.- 879 : 3 =
D.- 942 : 3 =
Una vez que has resuelto estas operaciones, llega el momento de empezar con la tabla del 4.
a.- Completa:
4x3=
2x4=
4x1=
4x5=
Hasta aquí ya deberías sabértelas. ¿ Qué nos tenemos que aprender? Resuelve y estudia:
4x4=
4x6=
4x7=
4x8=
4x9=
Piensa un poco:
¿ Qué número de la tabla del 4 da 16?¿Y 24 ? ¿Y 28?
Completa:
4x... = 4
4x ...= 16
4x... = 24
4x ...= 28
Coloca correctamente y resuelve:
a.- 467x4 =
b.- 764x4 =
c.- 667x4 =
d.- 776x4 =
e.- 766x4 =
Dale un poco al coco.
Nino Vargas y sus 3 amigos van al supermercado y compra 20 latas de refrescos con un importe total de 16,16€. ¿ Cuánto dinero tendrá que poner cada uno si pagan a partes iguales?
Cálculo
Realiza las siguientes operaciones:
a.- 89,45 + 9,8 + 234,6 =
b.- 9,92 + 2,9 + 9,34 =
c.- 234 - 123 =
d.- 563 - 498 =
e.- 934 - 927 =
f.- 234 X 2 =
g.- 398 X 2 =
h.- 928 : 2 =
i .- 879 : 2 =
j.- 942 : 2 =
División por 3.
a.- 124:3 =
b.- 456:3 =
c.- 893 : 3 =
d.- 983 : 3 =
e.- 993 : 3 =
f.- 2721 : 3 =
g.- 2727 : 3 =
h.- 2427 : 3 =
i.- 3221 : 3 =
j .- 2127 : 3 =
Resuelve las siguientes Potencias
84 = 94 =
82 = 73 =
83 = 75 =
| an . am = an+m | 83.85 = 83+5 = 88 92.95 = 73.73 = 62.63 = 87.82 = |
Suscribirse a:
Entradas (Atom)
Lo + del mes.
-
Lecturas comprensivas , una ficha interactiva de MimiEduca live worksheets.com
-
Comprensión lectora , una ficha interactiva de Teacher_Lidiaa live worksheets.com
